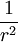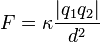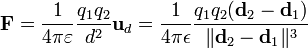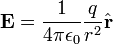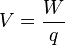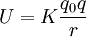ELECTROSTATICA
El estudiante deberà conocer previamente los siguientes conceptos:
- Propiedades de las Cargas Elèctricas.
- Inducciòn Electrostàtica.


Variación de la Fuerza de Coulomb en función de la distancia.


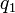 y
y 


en consecuencia:


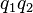
Asociando ambas relaciones:



Finalmente, se introduce una constante de proporcionalidad para transformar la relación anterior en una igualdad:
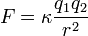

Representación gráfica de la Ley de Coulomb para dos cargas del mismo signo.
La constante
La constante, si las unidades de las cargas se encuentran en Coulomb es la siguiente K = 9 * 109 * N * m2 / C2 y su resultado será en sistema MKS (N / C). En cambio, si la unidad de las cargas están en UES (q), la constante se expresa de la siguiente forma K = d * m2 / ues(q) y su resultado estará en las unidades CGS (D / UES(q)).
Campo Elèctrico (E)
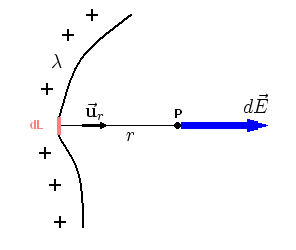

Campo eléctrico de una distribución lineal de carga.
Una carga puntual P es sometida a una fuerza en direccion radial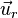 por una distribucion de carga λ en forma de diferencial de linea (dL), lo que produce un campo eléctrico
por una distribucion de carga λ en forma de diferencial de linea (dL), lo que produce un campo eléctrico  .
.
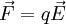
Ahora bien, si se pretende mantener la partícula en equilibrio, o desplazarla a velocidad constante, se requiere de una fuerza que contrarreste el efecto de la generada por el campo eléctrico. Esta fuerza deberá tener la misma magnitud que la primera, pero sentido contrario, es decir:
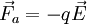 (1)
(1) 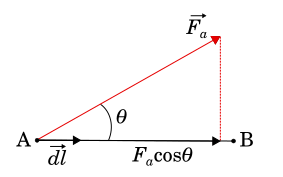
Partiendo de la definición clásica de trabajo, en este caso se realizará un trabajo para trasladar la carga de un punto a otro.De tal forma que al producirse un pequeño desplazamiento dl se generará un trabajo dW. Es importante resaltar que el trabajo será positivo o negativo dependiendo de cómo se realice el desplazamiento en relación con la fuerza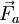 . El trabajo queda, entonces, expresado como:
. El trabajo queda, entonces, expresado como:

Nótese que en el caso de que la fuerza no esté en la dirección del desplazamiento, sólo se debe multiplicar su componente en la dirección del movimiento.
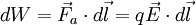
Por lo tanto, el trabajo total será:
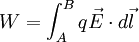
Si el trabajo que se realiza en cualquiera trayectoria cerrada es igual a cero, entonces se dice que estamos en presencia de un campo eléctrico conservativo.

Ahora bien, sea una carga q que recorre una determinada trayectoria en las inmediaciones de una carga Q tal como muestra la figura.

El trabajo infinitesimal es el producto escalar del vector fuerza F por el vector desplazamiento dl, tangente a la trayectoria, o sea:
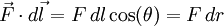
donde dr es el desplazamiento infinitesimal de la carga q en la dirección radial.
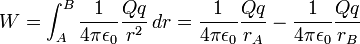
De lo anterior se concluye que el trabajo W no depende del camino seguido por la partícula para ir desde la posición A a la posición B. lo cual implica que la fuerza de atracción F, que ejerce la carga Q sobre la carga q es conservativa. La fórmula de la energía potencial es:
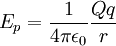
Por definición, el nivel cero de energía potencial se ha establecido en el infinito, o sea, si y sólo si .
.
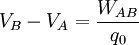
El trabajo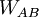 puede ser positivo, negativo o nulo. En estos casos el potencial eléctrico en B será respectivamente mayor, menor o igual que el potencial eléctrico en A. La unidad en el SI para la diferencia de potencial que se deduce de la ecuación anterior es Joule/Coulomb y se representa mediante una nueva unidad, el voltio, esto es: 1 voltio = 1 joule/coulomb.
puede ser positivo, negativo o nulo. En estos casos el potencial eléctrico en B será respectivamente mayor, menor o igual que el potencial eléctrico en A. La unidad en el SI para la diferencia de potencial que se deduce de la ecuación anterior es Joule/Coulomb y se representa mediante una nueva unidad, el voltio, esto es: 1 voltio = 1 joule/coulomb.
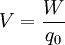
siendo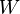 el trabajo que debe hacer un agente exterior para mover la carga de prueba
el trabajo que debe hacer un agente exterior para mover la carga de prueba  desde el infinito al punto en cuestión.
desde el infinito al punto en cuestión. 
Una carga de prueba se mueve desde A hasta B en el campo de carga q siguiendo una de dos trayectorias. Las flechas muestran a E en tres puntos de la trayectoria II

Una carga de prueba q se mueve de A hacia B en un campo eléctrico uniforme E mediante un agente exterior que ejerce sobre ella una fuerza F.
Considérese una carga de prueba positiva q moviéndose sin aceleración, por efecto de algún agente externo, siguiendo la recta que une A con B.

Teniendo en cuenta que:
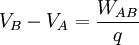
sustituyendo eso que esta mal se obtiene:
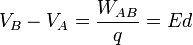
Esta ecuación muestra la relación entre la diferencia de potencial y la intensidad de campo en un caso sencillo especial.
Ejercicio 1 (Propuesto) : Dos cargas puntuales q1= 3*10-6C y q2= 4*10-6C estan separadas 0,5 m y ubicadas en el vacio.
Ejercicio 2:
Desarrollo
rm = 2*10-1 m/2
rm = 10-1 m
a) F1 = k*q1.q/rm ² y F2 = k*q2.q/rm ²
E = F/q
E = (F1 + F2)/q
E = (k*q1.q/rm ² + k*q2.q/rm ²)/q
E = q*k*(q1 + q2)/q.rm ²
E = k*(q1 + q2)/rm ²
E = 9*109 (Nm ²/C ²).(10-4 C - 5*10-5 C)/(10-1 m) ²
E = 9*109 (Nm ²/C ²) 5*10-5 C/10-2 m ²
E = 4,5*107 N/C
b) si q1 = q2 = -5*10-5 C
E = k*(q1 + q2)/rm ²
E = k*2*q1/rm ²
E = 9*109 (Nm ²/C ²) *2(- 5*10-5 C)/(10-1 m) ²
E = -9*109 (Nm ²/C ²)*10-4 C/10-2 m ²
E = -9*107 N/C
Ejercicio 3 ( propuesto) : Determina la carga de una partícula puntual sometida a un potencial eléctrico de otra carga de 127 V situada a 20 cm.
Referencias Bibliográficas:
http://es.wikipedia.org/wiki/ley_de_coulomb
http://es.wikipedia.org/wiki/campo_electrico
http://es.wikipedia.org/wiki/potencial_electrico
- Propiedades de las Cargas Elèctricas.
- Inducciòn Electrostàtica.
Ley de Coulomb
La ley de Coulomb puede expresarse como:
- La magnitud de cada una de las fuerzas eléctricas con que interactúan dos cargas puntuales en reposo es directamente proporcional al producto de la magnitud de ambas cargas e inversamente proporcional al cuadrado de la distancia que las separa.
Desarrollo de la ley
Charles-Augustin de Coulomb desarrolló la balanza de torsión con la que determinó las propiedades de la fuerza electrostática. Este instrumento consiste en una barra que cuelga de una fibra capaz de torcerse. Si la barra gira, la fibra tiende a hacerla regresar a su posición original, con lo que conociendo la fuerza de torsión que la fibra ejerce sobre la barra, se puede determinar la fuerza ejercida en un punto de la barra. La ley de Coulomb también conocida como ley de cargas tiene que ver con las cargas eléctricas de un material, es decir, depende de si sus cargas son negativas o positivas.

Variación de la Fuerza de Coulomb en función de la distancia.
En la barra de la balanza, Coulomb colocó una pequeña esfera cargada y a continuación, a diferentes distancias, posicionó otra esfera también cargada. Luego midió la fuerza entre ellas observando el ángulo que giraba la barra.
Dichas mediciones permitieron determinar que:
- La fuerza de interacción entre dos cargas
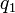 y
y  duplica su magnitud si alguna de las cargas dobla su valor, la triplica si alguna de las cargas aumenta su valor en un factor de tres, y así sucesivamente. Concluyó entonces que el valor de la fuerza era proporcional al producto de las cargas:
duplica su magnitud si alguna de las cargas dobla su valor, la triplica si alguna de las cargas aumenta su valor en un factor de tres, y así sucesivamente. Concluyó entonces que el valor de la fuerza era proporcional al producto de las cargas:


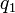 y
y 


en consecuencia:


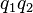
- Si la distancia entre las cargas es
 , al duplicarla, la fuerza de interacción disminuye en un factor de 4 (2²); al triplicarla, disminuye en un factor de 9 (3²) y al cuadriplicar
, al duplicarla, la fuerza de interacción disminuye en un factor de 4 (2²); al triplicarla, disminuye en un factor de 9 (3²) y al cuadriplicar  , la fuerza entre cargas disminuye en un factor de 16 (4²). En consecuencia, la fuerza de interacción entre dos cargas puntuales, es inversamente proporcional al cuadrado de la distancia:
, la fuerza entre cargas disminuye en un factor de 16 (4²). En consecuencia, la fuerza de interacción entre dos cargas puntuales, es inversamente proporcional al cuadrado de la distancia:



Finalmente, se introduce una constante de proporcionalidad para transformar la relación anterior en una igualdad:
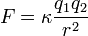
Enunciado de la ley
La ley de Coulomb es válida sólo en condiciones estacionarias, es decir, cuando no hay movimiento de las cargas o, como aproximación cuando el movimiento se realiza a velocidades bajas y en trayectorias rectilíneas uniformes. Es por ello que es llamada fuerza electrostática.
En términos matemáticos, la magnitud  de la fuerza que cada una de las dos cargas puntuales
de la fuerza que cada una de las dos cargas puntuales 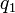 y
y  ejerce sobre la otra separadas por una distancia
ejerce sobre la otra separadas por una distancia  se expresa como:
se expresa como:
 de la fuerza que cada una de las dos cargas puntuales
de la fuerza que cada una de las dos cargas puntuales 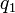 y
y  ejerce sobre la otra separadas por una distancia
ejerce sobre la otra separadas por una distancia  se expresa como:
se expresa como: Dadas dos cargas puntuales 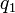 y
y  separadas una distancia
separadas una distancia  en el vacío, se atraen o repelen entre sí con una fuerza cuya magnitud está dada por:
en el vacío, se atraen o repelen entre sí con una fuerza cuya magnitud está dada por:
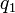 y
y  separadas una distancia
separadas una distancia  en el vacío, se atraen o repelen entre sí con una fuerza cuya magnitud está dada por:
en el vacío, se atraen o repelen entre sí con una fuerza cuya magnitud está dada por: La Ley de Coulomb se expresa mejor con magnitudes vectoriales:
donde  es un vector unitario que va en la dirección de la recta que une las cargas, siendo su sentido desde la carga que produce la fuerza hacia la carga que la experimenta.
es un vector unitario que va en la dirección de la recta que une las cargas, siendo su sentido desde la carga que produce la fuerza hacia la carga que la experimenta.
 es un vector unitario que va en la dirección de la recta que une las cargas, siendo su sentido desde la carga que produce la fuerza hacia la carga que la experimenta.
es un vector unitario que va en la dirección de la recta que une las cargas, siendo su sentido desde la carga que produce la fuerza hacia la carga que la experimenta. Al aplicar esta fórmula en un ejercicio, se debe colocar el signo de las cargas q1 o q2, según sean éstas positivas o negativas.
El exponente (de la distancia: d) de la Ley de Coulomb es, hasta donde se sabe hoy en día, exactamente 2. Experimentalmente se sabe que, si el exponente fuera de la forma 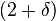 , entonces
, entonces 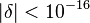
.
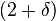 , entonces
, entonces 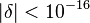
.
Representación gráfica de la Ley de Coulomb para dos cargas del mismo signo.
Obsérvese que esto satisface la tercera de la ley de Newton debido a que implica que fuerzas de igual magnitud actúan sobre 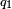 y
y  . La ley de Coulomb es una ecuación vectorial e incluye el hecho de que la fuerza actúa a lo largo de la línea de unión entre las cargas.
. La ley de Coulomb es una ecuación vectorial e incluye el hecho de que la fuerza actúa a lo largo de la línea de unión entre las cargas.
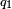 y
y  . La ley de Coulomb es una ecuación vectorial e incluye el hecho de que la fuerza actúa a lo largo de la línea de unión entre las cargas.
. La ley de Coulomb es una ecuación vectorial e incluye el hecho de que la fuerza actúa a lo largo de la línea de unión entre las cargas.Constante de Coulomb
La constante 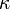 es la Constante de Coulomb y su valor para unidades SI es
es la Constante de Coulomb y su valor para unidades SI es 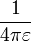 Nm²/C².
Nm²/C².
A su vez la constante  donde
donde 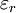 es la permitividad relativa,
es la permitividad relativa,  , y
, y 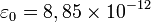 F/m es la permitividad del medio en el vacío.
F/m es la permitividad del medio en el vacío.
 donde
donde 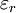 es la permitividad relativa,
es la permitividad relativa,  , y
, y 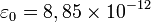 F/m es la permitividad del medio en el vacío.
F/m es la permitividad del medio en el vacío. Cuando el medio que rodea a las cargas no es el vacío hay que tener en cuenta la constante dieléctrica y la permitividad del material.
La ecuación de la ley de Coulomb queda finalmente expresada de la siguiente manera:
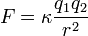 |
|---|
La constante, si las unidades de las cargas se encuentran en Coulomb es la siguiente K = 9 * 109 * N * m2 / C2 y su resultado será en sistema MKS (N / C). En cambio, si la unidad de las cargas están en UES (q), la constante se expresa de la siguiente forma K = d * m2 / ues(q) y su resultado estará en las unidades CGS (D / UES(q)).
El campo eléctrico es un campo físico que es representado mediante un modelo que describe la interacción entre cuerpos y sistemas con propiedades de naturaleza eléctrica.[1] Matemáticamente se describe como un campo vectorial en el cual una carga eléctrica puntual de valor q sufre los efectos de una fuerza eléctrica 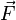 dada por la siguiente ecuación:
dada por la siguiente ecuación:
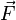 dada por la siguiente ecuación:
dada por la siguiente ecuación: (1)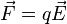
En los modelos relativistas actuales, el campo eléctrico se incorpora, junto con el campo magnético, en campo tensorial cuadridimensional, denominado campo electromagnético Fμν.[2]
Los campos eléctricos pueden tener su origen tanto en cargas eléctricas como en campos magnéticos variables. Las primeras descripciones de los fenómenos eléctricos, como la ley de Coulomb, sólo tenían en cuenta las cargas eléctricas, pero las investigaciones de Michael Faraday y los estudios posteriores de James Clerk Maxwell permitieron establecer las leyes completas en las que también se tiene en cuenta la variación del campo magnético.
Esta definición general indica que el campo no es directamente medible, sino que lo que es observable es su efecto sobre alguna carga colocada en su seno. La idea de campo eléctrico fue propuesta por Faraday al demostrar el principio de inducción electromagnética en el año 1832.
La unidad del campo eléctrico en el SI es Newton por Culombio (N/C), Voltio por metro (V/m) o, en unidades básicas, kg·m·s−3·A−1.
Definición
La definición más intuitiva acerca del campo eléctrico se la puede estudiar mediante la ley de Coulomb. Esta ley, una vez generalizada, permite expresar el campo entre distribuciones de carga en reposo relativo. Sin embargo, para cargas en movimiento una definición más formal y completa acerca del campo requiere el uso de cuadrivectores y el principio de mínima acción.
Definición mediante la ley de Coulomb
Campo eléctrico de una distribución lineal de carga.
Una carga puntual P es sometida a una fuerza en direccion radial
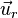 por una distribucion de carga λ en forma de diferencial de linea (dL), lo que produce un campo eléctrico
por una distribucion de carga λ en forma de diferencial de linea (dL), lo que produce un campo eléctrico  .
. Partiendo de la ley de Coulomb que expresa que la fuerza entre dos cargas en reposo relativo depende del cuadrado de la distancia, matemáticamente es igual a:[1]
Donde:
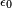 es la permitividad eléctrica del vacío tiene que ver con el sistema internacional,
es la permitividad eléctrica del vacío tiene que ver con el sistema internacional, son las cargas que interactúan,
son las cargas que interactúan,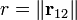 es la distancia entre ambas cargas,
es la distancia entre ambas cargas, , es el vector de posición relativa de la carga 2 respecto a la carga 1. y
, es el vector de posición relativa de la carga 2 respecto a la carga 1. y  es el unitario en la dirección
es el unitario en la dirección 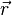 . Nótese que en la fórmula se está usando ε0, esta es la permitividad en el vacío. Para calcular la interacción en otro medio es necesario cambiar la permitividad de dicho medio. (ε = εr.ε0)
. Nótese que en la fórmula se está usando ε0, esta es la permitividad en el vacío. Para calcular la interacción en otro medio es necesario cambiar la permitividad de dicho medio. (ε = εr.ε0)
La ley anterior presuponía que la posición de una partícula en un instante dado, hace que su campo eléctrico afecte en el mismo instante a cualquier otra carga. Ese tipo de interacciónes en las que el efecto sobre el resto de partículas parece dependender sólo de la posición de la partícula causante sin importar la distancia entre las partículas se denomina en física acción a distancia. Si bien la noción de acción a distancia fue aceptada inicialmente por el propio Newton, experimentos más cuidados a lo largo del siglo XIX llevaron a desechar dicha noción como no-realista. En ese contexto se pensó que el campo eléctrico no sólo era un artificio matemático sino un ente físico que se propaga a una velocidad finita (la velocidad de la luz) hasta afectar a otras partículas. Esa idea conllevaba modificar la ley de Coulomb de acuerdo con los requerimientos de la teoría de la relatividad y dotar de entidad física al campo eléctrico.[1] Así, el campo eléctrico es una distorsión electromagnética que sufre el espacio debido a la presencia de una carga. Considerando esto se puede obtener una expresión del campo eléctrico cuando este sólo depende de la distancia entre las cargas:
Donde claramente se tiene que  , la que es una de las definiciones más conocidas acerca del campo eléctrico.
, la que es una de las definiciones más conocidas acerca del campo eléctrico.
 , la que es una de las definiciones más conocidas acerca del campo eléctrico.
, la que es una de las definiciones más conocidas acerca del campo eléctrico. Potencial Elèctrico (V)
El potencial eléctrico en un punto es el trabajo que debe realizar una fuerza eléctrica para mover una carga positiva q desde la referencia hasta ese punto, dividido por unidad de carga de prueba. Dicho de otra forma, es el trabajo que debe realizar una fuerza externa para traer una carga unitaria q desde la referencia hasta el punto considerado en contra de la fuerza eléctrica. Matemáticamente se expresa por:
Considérese una carga puntual de prueba positiva, la cual se puede utilizar para hacer el mapa de un campo eléctrico. Para tal carga de prueba  localizada a una distancia r de una carga q, la energía potencial electrostática mutua es:
localizada a una distancia r de una carga q, la energía potencial electrostática mutua es:
 localizada a una distancia r de una carga q, la energía potencial electrostática mutua es:
localizada a una distancia r de una carga q, la energía potencial electrostática mutua es: De manera equivalente, el potencial eléctrico es  =
= 
 =
= 
Trabajo eléctrico y energía potencial eléctrica
Considérese una carga puntual q en presencia de un campo eléctrico. La carga experimentará una fuerza eléctrica.
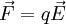
Ahora bien, si se pretende mantener la partícula en equilibrio, o desplazarla a velocidad constante, se requiere de una fuerza que contrarreste el efecto de la generada por el campo eléctrico. Esta fuerza deberá tener la misma magnitud que la primera, pero sentido contrario, es decir:
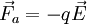 (1)
(1)
Partiendo de la definición clásica de trabajo, en este caso se realizará un trabajo para trasladar la carga de un punto a otro.De tal forma que al producirse un pequeño desplazamiento dl se generará un trabajo dW. Es importante resaltar que el trabajo será positivo o negativo dependiendo de cómo se realice el desplazamiento en relación con la fuerza
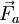 . El trabajo queda, entonces, expresado como:
. El trabajo queda, entonces, expresado como: 
Nótese que en el caso de que la fuerza no esté en la dirección del desplazamiento, sólo se debe multiplicar su componente en la dirección del movimiento.
Será considerado trabajo positivo el realizado por un agente externo al sistema carga-campo que ocasione un cambio de posición y negativo aquél que realice el campo.
Teniendo en cuenta la expresión (1):
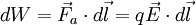
Por lo tanto, el trabajo total será:
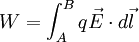
Si el trabajo que se realiza en cualquiera trayectoria cerrada es igual a cero, entonces se dice que estamos en presencia de un campo eléctrico conservativo.
Expresándolo matemáticamente

Ahora bien, sea una carga q que recorre una determinada trayectoria en las inmediaciones de una carga Q tal como muestra la figura.

El trabajo infinitesimal es el producto escalar del vector fuerza F por el vector desplazamiento dl, tangente a la trayectoria, o sea:
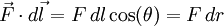
donde dr es el desplazamiento infinitesimal de la carga q en la dirección radial.
Para calcular el trabajo total, se integra entre la posición inicial A, distante 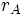 del centro de fuerzas y la posición final B, distante
del centro de fuerzas y la posición final B, distante  del centro fijo de fuerzas:
del centro fijo de fuerzas:
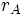 del centro de fuerzas y la posición final B, distante
del centro de fuerzas y la posición final B, distante  del centro fijo de fuerzas:
del centro fijo de fuerzas: 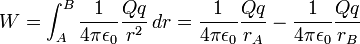
De lo anterior se concluye que el trabajo W no depende del camino seguido por la partícula para ir desde la posición A a la posición B. lo cual implica que la fuerza de atracción F, que ejerce la carga Q sobre la carga q es conservativa. La fórmula de la energía potencial es:
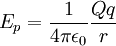
Por definición, el nivel cero de energía potencial se ha establecido en el infinito, o sea, si y sólo si
 .
. Diferencia de Potencial eléctrico
Considérese una carga de prueba positiva  en presencia de un campo eléctrico y que se traslada desde el punto A al punto B conservándose siempre en equilibrio. Si se mide el trabajo que debe hacer el agente que mueve la carga, la diferencia de potencial eléctrico se define como:
en presencia de un campo eléctrico y que se traslada desde el punto A al punto B conservándose siempre en equilibrio. Si se mide el trabajo que debe hacer el agente que mueve la carga, la diferencia de potencial eléctrico se define como:
 en presencia de un campo eléctrico y que se traslada desde el punto A al punto B conservándose siempre en equilibrio. Si se mide el trabajo que debe hacer el agente que mueve la carga, la diferencia de potencial eléctrico se define como:
en presencia de un campo eléctrico y que se traslada desde el punto A al punto B conservándose siempre en equilibrio. Si se mide el trabajo que debe hacer el agente que mueve la carga, la diferencia de potencial eléctrico se define como: 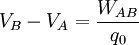
El trabajo
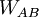 puede ser positivo, negativo o nulo. En estos casos el potencial eléctrico en B será respectivamente mayor, menor o igual que el potencial eléctrico en A. La unidad en el SI para la diferencia de potencial que se deduce de la ecuación anterior es Joule/Coulomb y se representa mediante una nueva unidad, el voltio, esto es: 1 voltio = 1 joule/coulomb.
puede ser positivo, negativo o nulo. En estos casos el potencial eléctrico en B será respectivamente mayor, menor o igual que el potencial eléctrico en A. La unidad en el SI para la diferencia de potencial que se deduce de la ecuación anterior es Joule/Coulomb y se representa mediante una nueva unidad, el voltio, esto es: 1 voltio = 1 joule/coulomb. Un electronvoltio (eV) es la energía adquirida para un electrón al moverse a través de una diferencia de potencial de 1 V, 1 eV = 1,6x10-19 J. Algunas veces se necesitan unidades mayores de energía, y se usan los kiloelectronvoltios (keV), megaelectronvoltios (MeV) y los gigaelectronvoltios (GeV). (1 keV=103 eV, 1 MeV = 106 eV, y 1 GeV = 109 eV).
Aplicando esta definición a la teoría de circuitos y desde un punto de vista más intuitivo, se puede decir que el potencial eléctrico en un punto de un circuito representa la energía que posee cada unidad de carga al paso por dicho punto. Así, si dicha unidad de carga recorre un circuito constituyendóse en corriente eléctrica, ésta irá perdiendo su energía (potencial o voltaje) a medida que atraviesa los diferentes componentes del mismo. Obviamente, la energía perdida por cada unidad de carga se manifestará como trabajo realizado en dicho circuito (calentamiento en una resistencia, luz en una lámpara, movimiento en un motor, etc.). Por el contrario, esta energía perdida se recupera al paso por fuentes generadoras de tensión. Es conveniente distinguir entre potencial eléctrico en un punto (energía por unidad de carga situada en ese punto) y corriente eléctrica (número de cargas que atraviesan dicho punto por segundo).
Usualmente se escoge el punto A a una gran distancia (en rigor el infinito) de toda carga y el potencial eléctrico  a esta distancia infinita recibe arbitrariamente el valor cero. Esto permite definir el potencial eléctrico en un punto poniendo
a esta distancia infinita recibe arbitrariamente el valor cero. Esto permite definir el potencial eléctrico en un punto poniendo 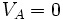 y eliminando los índices:
y eliminando los índices:
 a esta distancia infinita recibe arbitrariamente el valor cero. Esto permite definir el potencial eléctrico en un punto poniendo
a esta distancia infinita recibe arbitrariamente el valor cero. Esto permite definir el potencial eléctrico en un punto poniendo 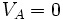 y eliminando los índices:
y eliminando los índices: 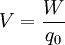
siendo
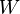 el trabajo que debe hacer un agente exterior para mover la carga de prueba
el trabajo que debe hacer un agente exterior para mover la carga de prueba  desde el infinito al punto en cuestión.
desde el infinito al punto en cuestión. Obsérvese que la igualdad planteada depende de que se da arbitrariamente el valor cero al potencial  en la posición de referencia (el infinito) el cual hubiera podido escogerse de cualquier otro valor así como también se hubiera podido seleccionar cualquier otro punto de referencia.
en la posición de referencia (el infinito) el cual hubiera podido escogerse de cualquier otro valor así como también se hubiera podido seleccionar cualquier otro punto de referencia.
 en la posición de referencia (el infinito) el cual hubiera podido escogerse de cualquier otro valor así como también se hubiera podido seleccionar cualquier otro punto de referencia.
en la posición de referencia (el infinito) el cual hubiera podido escogerse de cualquier otro valor así como también se hubiera podido seleccionar cualquier otro punto de referencia. También es de hacer notar que según la expresión que define el potencial eléctrico en un punto, el potencial en un punto cercano a una carga positiva aislada es positivo porque debe hacerse trabajo positivo mediante un agente exterior para llevar al punto una carga de prueba (positiva) desde el infinito. Similarmente, el potencial cerca de una carga negativa aislada es negativo porque un agente exterior debe ejercer una fuerza (trabajo negativo en este caso) para sostener a la carga de prueba (positiva) cuando esta (la carga positiva) viene desde el infinito.
Por último, el potencial eléctrico queda definido como un escalar porque 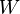 y
y  son escalares.
son escalares.
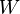 y
y  son escalares.
son escalares. Tanto 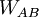 como
como 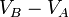 son independientes de la trayectoria que se siga al mover la carga de prueba desde el punto A hasta el punto B. Si no fuera así, el punto B no tendría un potencial eléctrico único con respecto al punto A y el concepto de potencial sería de utilidad restringida.
son independientes de la trayectoria que se siga al mover la carga de prueba desde el punto A hasta el punto B. Si no fuera así, el punto B no tendría un potencial eléctrico único con respecto al punto A y el concepto de potencial sería de utilidad restringida.
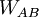 como
como 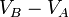 son independientes de la trayectoria que se siga al mover la carga de prueba desde el punto A hasta el punto B. Si no fuera así, el punto B no tendría un potencial eléctrico único con respecto al punto A y el concepto de potencial sería de utilidad restringida.
son independientes de la trayectoria que se siga al mover la carga de prueba desde el punto A hasta el punto B. Si no fuera así, el punto B no tendría un potencial eléctrico único con respecto al punto A y el concepto de potencial sería de utilidad restringida.Una carga de prueba se mueve desde A hasta B en el campo de carga q siguiendo una de dos trayectorias. Las flechas muestran a E en tres puntos de la trayectoria II
Es posible demostrar que las diferencias de potencial son independientes de la trayectoria para el caso especial representado en la figura. Para mayor simplicidad se han escogido los puntos A y B en una recta radial.
Una carga de prueba puede trasladarse desde A hacia B siguiendo la trayectoria I sobre una recta radial o la trayectoria II completamente arbitraria.
La trayectoria II puede considerarse equivalente a una trayectoria quebrada formada por secciones de arco y secciones radiales alternadas. Puesto que estas secciones se pueden hacer tan pequeñas como se desee, la trayectoria quebrada puede aproximarse a la trayectoria II tanto como se quiera. En la trayectoria II el agente externo hace trabajo solamente a lo largo de las secciones radiales, porque a lo largo de los arcos, la fuerza  y el corrimiento
y el corrimiento 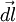 son perpendiculares y en tales casos
son perpendiculares y en tales casos 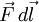 es nulo. La suma del trabajo hecho en los segmentos radiales que constituyen la trayectoria II es el mismo que el trabajo efectuado en la trayectoria I, porque cada trayectoria está compuesta del mismo conjunto de segmentos radiales. Como la trayectoria II es arbitraria, se ha demostrado que el trabajo realizado es el mismo para todas las trayectorias que unen A con B.
es nulo. La suma del trabajo hecho en los segmentos radiales que constituyen la trayectoria II es el mismo que el trabajo efectuado en la trayectoria I, porque cada trayectoria está compuesta del mismo conjunto de segmentos radiales. Como la trayectoria II es arbitraria, se ha demostrado que el trabajo realizado es el mismo para todas las trayectorias que unen A con B.
 y el corrimiento
y el corrimiento 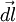 son perpendiculares y en tales casos
son perpendiculares y en tales casos 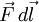 es nulo. La suma del trabajo hecho en los segmentos radiales que constituyen la trayectoria II es el mismo que el trabajo efectuado en la trayectoria I, porque cada trayectoria está compuesta del mismo conjunto de segmentos radiales. Como la trayectoria II es arbitraria, se ha demostrado que el trabajo realizado es el mismo para todas las trayectorias que unen A con B.
es nulo. La suma del trabajo hecho en los segmentos radiales que constituyen la trayectoria II es el mismo que el trabajo efectuado en la trayectoria I, porque cada trayectoria está compuesta del mismo conjunto de segmentos radiales. Como la trayectoria II es arbitraria, se ha demostrado que el trabajo realizado es el mismo para todas las trayectorias que unen A con B. Aun cuando esta prueba sólo es válida para el caso especial ilustrado en la figura, la diferencia de potencial es independiente de la trayectoria para dos puntos cualesquiera en cualquier campo eléctrico. Se desprende de ello el carácter conservativo de la interacción electrostática el cual está asociado a la naturaleza central de las fuerzas electrostáticas.
Para un par de placas paralelas en las cuales se cumple que 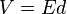 , donde d es la distancia entre las placas paralelas y E es el campo eléctrico constante en la región entre las placas.
, donde d es la distancia entre las placas paralelas y E es el campo eléctrico constante en la región entre las placas.
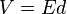 , donde d es la distancia entre las placas paralelas y E es el campo eléctrico constante en la región entre las placas.
, donde d es la distancia entre las placas paralelas y E es el campo eléctrico constante en la región entre las placas. Campo eléctrico uniforme
Sean A y B dos puntos situados en un campo eléctrico uniforme, estando A a una distancia d de B en la dirección del campo, tal como muestra la figura.
Una carga de prueba q se mueve de A hacia B en un campo eléctrico uniforme E mediante un agente exterior que ejerce sobre ella una fuerza F.
Considérese una carga de prueba positiva q moviéndose sin aceleración, por efecto de algún agente externo, siguiendo la recta que une A con B.
La fuerza eléctrica sobre la carga será qE y apunta hacia abajo. Para mover la carga en la forma descrita arriba, se debe contrarrestar esa fuerza aplicando una fuerza externa F de la misma magnitud pero dirigida hacia arriba. El trabajo 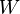 realizado por el agente que proporciona esta fuerza es:
realizado por el agente que proporciona esta fuerza es:
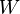 realizado por el agente que proporciona esta fuerza es:
realizado por el agente que proporciona esta fuerza es: 
Teniendo en cuenta que:
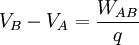
sustituyendo eso que esta mal se obtiene:
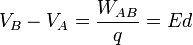
Esta ecuación muestra la relación entre la diferencia de potencial y la intensidad de campo en un caso sencillo especial.
El punto B tiene un potencial más elevado que el A. Esto es razonable porque un agente exterior tendría que hacer trabajo positivo para mover la carga de prueba de A hacia B.
Ejercicios
Ejercicio 1 (Propuesto) : Dos cargas puntuales q1= 3*10-6C y q2= 4*10-6C estan separadas 0,5 m y ubicadas en el vacio.
a) Calcule el valor de la fuerza entre las cargas.
b) Construya un esquema donde represente la situacion anterior y las fuerzas de interaccion entre las cargas.
Ejercicio 2:
a) ¿Cuál es la intensidad del campo eléctrico en un punto colocado a la mitad entre una carga positiva de 100 μ C y una negativa de 50 μ C separadas 20 cm?.
b) ¿Y si ambas fueran negativas de 50 μ C?.Desarrollo
Datos:
rm = r/2 q1 = 100 μ C = 10-4 C
q2 = -50 μ C = -5*10-5 C
r = 20 cm = 2*10-1 m
q2 = -50 μ C = -5*10-5 C
r = 20 cm = 2*10-1 m
rm = 2*10-1 m/2
rm = 10-1 m
a) F1 = k*q1.q/rm ² y F2 = k*q2.q/rm ²
E = F/q
E = (F1 + F2)/q
E = (k*q1.q/rm ² + k*q2.q/rm ²)/q
E = q*k*(q1 + q2)/q.rm ²
E = k*(q1 + q2)/rm ²
E = 9*109 (Nm ²/C ²).(10-4 C - 5*10-5 C)/(10-1 m) ²
E = 9*109 (Nm ²/C ²) 5*10-5 C/10-2 m ²
E = 4,5*107 N/C
b) si q1 = q2 = -5*10-5 C
E = k*(q1 + q2)/rm ²
E = k*2*q1/rm ²
E = 9*109 (Nm ²/C ²) *2(- 5*10-5 C)/(10-1 m) ²
E = -9*109 (Nm ²/C ²)*10-4 C/10-2 m ²
E = -9*107 N/C
Ejercicio 3 ( propuesto) : Determina la carga de una partícula puntual sometida a un potencial eléctrico de otra carga de 127 V situada a 20 cm.
Referencias Bibliográficas:
http://es.wikipedia.org/wiki/ley_de_coulomb
http://es.wikipedia.org/wiki/campo_electrico
http://es.wikipedia.org/wiki/potencial_electrico