CORRIENTE Y RESISTENCIA ELECTRICA
El estudiante deberà tener conocimientos previos de:
- Energìa potencial elèctrica.
- Potencial elèctrico.
- Diferencia de potencial (Voltaje)
Corriente Elèctrica

Según sea la magnitud de esta medida, los materiales se pueden clasificar en conductores, aislantes y semiconductor. Existen además ciertos materiales en los que, en determinadas condiciones de temperatura, aparece un fenómeno denominado superconductividad, en el que el valor de la resistencia es prácticamente nulo.
donde . Se obtiene así, para la corriente, una función senoidal que está en fase con la tensión aplicada.
. Se obtiene así, para la corriente, una función senoidal que está en fase con la tensión aplicada.


Figura 4. Asociaciones generales de resistencias: a) Serie y b) Paralelo. c) Resistencia equivalente.


Figura 5. Asociaciones mixtas de cuatro resistencias: a) Serie de paralelos, b) Paralelo de series y c) Ejemplo de una de las otras posibles conexiones.


Figura 6.
a) Asociación en estrella.
b) Asociación en triángulo.


Figura 7. Asociación puente.
El conductor es el encargado de unir eléctricamente cada uno de los componentes de un circuito. Dado que tiene resistencia óhmica, puede ser considerado como otro componente más con características similares a las de la resistencia eléctrica.
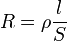

donde




Paso 2 . La resistencia serie del conjunto de 4 ohms y 16 ohms es ,

Fig. 1-9 . Pasos para resolver el circuito serie-paralelo ( problema 2) .
Paso 3. Para las resistencias de 20 ohms y 80 ohms en paralelo,

- Energìa potencial elèctrica.
- Potencial elèctrico.
- Diferencia de potencial (Voltaje)
Corriente Elèctrica
La corriente o intensidad eléctrica es el flujo de carga por unidad de tiempo que recorre un material. Se debe a un movimiento de los electrones en el interior del material. En el Sistema Internacional de Unidades se expresa en C/s (culombios sobre segundo), unidad que se denomina amperio. Una corriente eléctrica, puesto que se trata de un movimiento de cargas, produce un campo magnético, lo que se aprovecha en el electroimán.
El instrumento usado para medir la intensidad de la corriente eléctrica es el galvanómetro que, calibrado en amperios, se llama amperímetro, colocado en serie con el conductor cuya intensidad se desea medir.
Conducción eléctrica
Un material conductor posee gran cantidad de electrones libres, por lo que es posible el paso de la electricidad a través del mismo. Los electrones libres, aunque existen en el material, no se puede decir que pertenezcan a algún átomo determinado.
Una corriente de electricidad existe en un lugar cuando una carga neta se transporta desde ese lugar a otro en dicha región. Supongamos que la carga se mueve a través de un alambre. Si la carga q se transporta a través de una sección transversal dada del alambre, en un tiempo t, entonces la intensidad de corriente I, a través del alambre es:
Una característica de los electrones libres es que, incluso sin aplicarles un campo eléctrico desde afuera, se mueven a través del objeto de forma aleatoria debido a la energía calórica. En el caso de que no hayan aplicado ningún campo eléctrico, cumplen con la regla de que la media de estos movimientos aleatorios dentro del objeto es igual a cero. Esto es: dado un plano irreal trazado a través del objeto, si sumamos las cargas (electrones) que atraviesan dicho plano en un sentido, y sustraemos las cargas que lo recorren en sentido inverso, estas cantidades se anulan.
Cuando se aplica una fuente de tensión externa (como, por ejemplo, una batería) a los extremos de un material conductor, se está aplicando un campo eléctrico sobre los electrones libres. Este campo provoca el movimiento de los mismos en dirección al terminal positivo del material (los electrones son atraídos [tomados] por el terminal positivo y rechazados [inyectados] por el negativo). Es decir, los electrones libres son los portadores de la corriente eléctrica en los materiales conductores.
Si la intensidad es constante en el tiempo, se dice que la corriente es continua; en caso contrario, se llama variable. Si no se produce almacenamiento ni disminución de carga en ningún punto del conductor, la corriente es estacionaria.
Para obtener una corriente de 1 amperio, es necesario que 1 culombio de carga eléctrica por segundo esté atravesando un plano imaginario trazado en el material conductor.
El valor I de la intensidad instantánea será:
Si la intensidad permanece constante, en cuyo caso se denota Im, utilizando incrementos finitos de tiempo se puede definir como:
Si la intensidad es variable la fórmula anterior da el valor medio de la intensidad en el intervalo de tiempo considerado.
Según la ley de Ohm, la intensidad de la corriente es igual al voltaje dividido por la resistencia que oponen los cuerpos:
Haciendo referencia a la potencia, la intensidad equivale a la raíz cuadrada de la potencia dividida por la resistencia. En un circuito que contenga varios generadores y receptores, la intensidad es igual a:
donde Σε es el sumatorio de las fuerzas electromotrices del circuito, Σε' es la suma de todas la fuerzas contraelectromotrices, ΣR es la resistencia equivalente del circuito, Σr es la suma de las resistencias internas de los generadores y Σr' es el sumatorio de las resistencias internas de los receptores.
La Intensidad de corriente en un elemento de volumen serà:  , donde encontramos n como el número de cargas portadoras por unidad de volumen dV; q refiriéndose a la carga del portador; v la velocidad del portador y finalmente dS como el área de la sección del elemento de volumen del conductor.
, donde encontramos n como el número de cargas portadoras por unidad de volumen dV; q refiriéndose a la carga del portador; v la velocidad del portador y finalmente dS como el área de la sección del elemento de volumen del conductor.
 , donde encontramos n como el número de cargas portadoras por unidad de volumen dV; q refiriéndose a la carga del portador; v la velocidad del portador y finalmente dS como el área de la sección del elemento de volumen del conductor.
, donde encontramos n como el número de cargas portadoras por unidad de volumen dV; q refiriéndose a la carga del portador; v la velocidad del portador y finalmente dS como el área de la sección del elemento de volumen del conductor.Resistencia Elèctrica
La resistencia eléctrica de un objeto es una medida de su oposición al paso de corriente.
Descubierta por Georg Ohm en 1827, la resistencia eléctrica tiene un parecido conceptual a la fricción en la física mecánica. La unidad de la resistencia en el Sistema Internacional de Unidades es el ohmio (Ω). Para su medición en la práctica existen diversos métodos, entre los que se encuentra el uso de un ohmímetro. Además, su cantidad recíproca es la conductancia, medida en Siemens.
Para una gran cantidad de materiales y condiciones, la resistencia eléctrica depende de la corriente eléctrica que pasa a través de un objeto y de la tensión en los terminales de este. Esto significa que, dada una temperatura y un material, la resistencia es un valor que se mantendrá constante. Además, de acuerdo con la ley de Ohm la resistencia de un material puede definirse como la razón de la tensión y la corriente, así :

Según sea la magnitud de esta medida, los materiales se pueden clasificar en conductores, aislantes y semiconductor. Existen además ciertos materiales en los que, en determinadas condiciones de temperatura, aparece un fenómeno denominado superconductividad, en el que el valor de la resistencia es prácticamente nulo.
Comportamiento en corriente continua.
Una resistencia real en corriente continua (CC) se comporta prácticamente de la misma forma que si fuera ideal, esto es, transformando la energía eléctrica en calor por efecto Joule. La ley de Ohm para corriente continua establece que:
donde R es la resistencia en ohmios, V es la diferencia de potencial en voltios e I es la intensidad de corriente en amperios.
Comportamiento en corriente alterna
Como se ha comentado anteriormente, una resistencia real muestra un comportamiento diferente del que se observaría en una resistencia ideal si la intensidad que la atraviesa no es continua. En el caso de que la señal aplicada sea senoidal, corriente alterna (CA), a bajas frecuencias se observa que una resistencia real se comportará de forma muy similar a como lo haría en CC, siendo despreciables las diferencias. En altas frecuencias el comportamiento es diferente, aumentando en la medida en la que aumenta la frecuencia aplicada, lo que se explica fundamentalmente por los efectos inductivos que producen los materiales que conforman la resistencia real.
Por ejemplo, en una resistencia de carbón los efectos inductivos solo provienen de los propios terminales de conexión del dispositivo mientras que en una resistencia de tipo bobinado estos efectos se incrementan por el devanado de hilo resistivo alrededor del soporte cerámico, además de aparecer una cierta componente capacitiva si la frecuencia es especialmente elevada. En estos casos, para analizar los circuitos, la resistencia real se sustituye por una asociación serie formada por una resistencia ideal y por una bobina también ideal, aunque a veces también se les puede añadir un pequeño condensador ideal en paralelo con dicha asociación serie. En los conductores, además, aparecen otros efectos entre los que cabe destacar el efecto pelicular.
Consideremos una resistencia R, a la que se aplica una tensión alterna de valor:
De acuerdo con la ley de Ohm circulará una corriente alterna de valor:
donde
 . Se obtiene así, para la corriente, una función senoidal que está en fase con la tensión aplicada.
. Se obtiene así, para la corriente, una función senoidal que está en fase con la tensión aplicada. Si se representa el valor eficaz de la corriente obtenida en forma polar:
Y operando matemáticamente:
De donde se deduce que en los circuitos de CA la resistencia puede considerarse como una magnitud compleja con parte real y sin parte imaginaria o, lo que es lo mismo con argumento nulo, cuya representación binómica y polar serán:
Asociación de resistencias
Resistencia equivalente

Figura 4. Asociaciones generales de resistencias: a) Serie y b) Paralelo. c) Resistencia equivalente.
Se denomina resistencia equivalente de una asociación respecto de dos puntos A y B, a aquella que conectada a la misma diferencia de potencial, UAB, demanda la misma intensidad, I (ver figura 4). Esto significa que ante las mismas condiciones, la asociación y su resistencia equivalente disipan la misma potencia.
Asociación en serie
Dos o más resistencias se encuentran conectadas en serie cuando al aplicar al conjunto una diferencia de potencial, todas ellas son recorridas por la misma corriente.
Para determinar la resistencia equivalente de una asociación serie imaginaremos que ambas, figuras 4a) y 4c), están conectadas a la misma diferencia de potencial, UAB. Si aplicamos la segunda ley de Kirchhoff a la asociación en serie tendremos:
Aplicando la ley de Ohm:
En la resistencia equivalente:
Finalmente, igualando ambas ecuaciones se obtiene que:
Y eliminando la intensidad:
Por lo tanto, la resistencia equivalente a n resistencias montadas en serie es igual a la sumatoria de dichas resistencias.
Asociación en paralelo
Dos o más resistencias se encuentran en paralelo cuando tienen dos terminales comunes de modo que al aplicar al conjunto una diferencia de potencial, UAB, todas las resistencias tienen la misma caída de tensión, UAB.
Para determinar la resistencia equivalente de una asociación en paralelo imaginaremos que ambas, figuras 4b) y 4c), están conectadas a la misma diferencia de potencial mencionada, UAB, lo que originará una misma demanda de corriente eléctrica, I. Esta corriente se repartirá en la asociación por cada una de sus resistencias de acuerdo con la primera ley de Kirchhoff:
Aplicando la ley de Ohm:
En la resistencia equivalente se cumple:
Igualando ambas ecuaciones y eliminando la tensión UAB:
De donde:
Por lo que la resistencia equivalente de una asociación en paralelo es igual a la inversa de la suma de las inversas de cada una de las resistencias.
Existen dos casos particulares que suelen darse en una asociación en paralelo:
- 1. Dos resistencias: en este caso se puede comprobar que la resistencia equivalente es igual al producto dividido por la suma de sus valores, esto es:

- 2. k resistencias iguales: su equivalente resulta ser:

Asociación mixta

Figura 5. Asociaciones mixtas de cuatro resistencias: a) Serie de paralelos, b) Paralelo de series y c) Ejemplo de una de las otras posibles conexiones.
En una asociación mixta podemos encontrarnos conjuntos de resistencias en serie con conjuntos de resistencias en paralelo. En la figura 5 pueden observarse tres ejemplos de asociaciones mixtas con cuatro resistencias.
A veces una asociación mixta es necesaria ponerla en modo texto. Para ello se utilizan los símbolos "+" y "//" para designar las asociaciones serie y paralelo respectivamente. Así con (R1 + R2) se indica que R1 y R2 están en serie mientras que con (R1//R2) que están en paralelo. De acuerdo con ello, las asociaciones de la figura 5 se pondrían del siguiente modo:
- a) (R1//R2)+(R3//R4)
- b) (R1+R3)//(R2+R4)
- c) ((R1+R2)//R3)+R4
Para determinar la resistencia equivalente de una asociación mixta se van simplificando las resistencias que están en serie y las que están en paralelo de modo que el conjunto vaya resultando cada vez más sencillo, hasta terminar con un conjunto en serie o en paralelo. Como ejemplo se determinarán las resistencias equivalentes de cada una de las asociaciones de la figura 5:
- a)
- R1//R2 = R1//2
- R3//R4 = R3//4
- RAB = R1//2 + R3//4
- b)
- R1+R3 = R1+3
- R2+R4 = R2+4
- RAB = R1+3//R2+4
- c)
- R1+R2 = R1+2
- R1+2//R3 = R1+2//3
- RAB = R1+2//3 + R4
Desarrollando se obtiene:
- a)
- b)
- c)
Asociaciones estrella y triángulo
Artículo principal: Teorema de Kennelly
Figura 6.
a) Asociación en estrella.
b) Asociación en triángulo.
En la figura a) y b) pueden observarse respectivamente las asociaciones estrella y triángulo, también llamadas T y π o delta respectivamente. Este tipo de asociaciones son comunes en las cargas trifásicas. Las ecuaciones de equivalencia entre ambas asociaciones vienen dadas por el teorema de Kennelly:
- Resistencias en estrella en función de las resistencias en triángulo (transformación de triángulo a estrella)
El valor de cada una de las resistencias en estrella es igual al cociente del producto de las dos resistencias en triángulo adyacentes al mismo terminal entre la suma de las tres resistencias en triángulo.
- Resistencias en triángulo en función de las resistencias en estrella (transformación de estrella a triángulo)
El valor de cada una de las resistencias en triángulo es igual la suma de las dos resistencias en estrella adyacentes a los mismos terminales más el cociente del producto de esas dos resistencias entre la otra resistencia.
Asociación puente

Figura 7. Asociación puente.
Si en una asociación paralelo de series como la mostrada en la figura 5b se conecta una resistencia que una las dos ramas en paralelo, se obtiene una asociación puente como la mostrada en la figura 7.
La determinación de la resistencia equivalente de este tipo de asociación tiene sólo interés pedagógico. Para ello se sustituye bien una de las configuraciones en triángulo de la asociación, la R1-R2-R5 o la R3-R4-R5 por su equivalente en estrella, bien una de las configuraciones en estrella, la R1-R3-R5 o la R2-R4-R5 por su equivalente en triángulo. En ambos casos se consigue transformar el conjunto en una asociación mixta de cálculo sencillo. Otro método consiste en aplicar una fem (E) a la asociación y obtener su resistencia equivalente como relación de dicha fem y la corriente total demandada (E/I).
El interés de este tipo de asociación está en el caso en el que por la resistencia central, R5, no circula corriente, pues permite calcular los valores de una de las resistencias, R1, R2, R3 o R4, en función de las otras tres. En ello se basan los puentes de Wheatstone y de hilo para la medida de resistencias con precisión.
Resistencia de un conductor
| Material | Resistividad (Ω·m) |
|---|---|
| Plata[1] | 1,55 × 10–8 |
| Cobre[2] | 1,70 × 10–8 |
| Oro[3] | 2,22 × 10–8 |
| Aluminio[4] | 2,82 × 10–8 |
| Wolframio[5] | 5,65 × 10–8 |
| Níquel[6] | 6,40 × 10–8 |
| Hierro[7] | 8,90 × 10–8 |
| Platino[8] | 10,60 × 10–8 |
| Estaño[9] | 11,50 × 10–8 |
| Acero inoxidable 301[10] | 72,00 × 10–8 |
| Grafito[11] | 60,00 × 10–8 |
El conductor es el encargado de unir eléctricamente cada uno de los componentes de un circuito. Dado que tiene resistencia óhmica, puede ser considerado como otro componente más con características similares a las de la resistencia eléctrica.
De este modo, la resistencia de un conductor eléctrico es la medida de la oposición que presenta al movimiento de los electrones en su seno, o sea la oposición que presenta al paso de la corriente eléctrica. Generalmente su valor es muy pequeño y por ello se suele despreciar, esto es, se considera que su resistencia es nula (conductor ideal), pero habrá casos particulares en los que se deberá tener en cuenta su resistencia (conductor real).
La resistencia de un conductor depende de la longitud del mismo ( ) en m, de su sección (
) en m, de su sección ( ) en m², del tipo de material y de la temperatura. Si consideramos la temperatura constante (20 ºC), la resistencia viene dada por la siguiente expresión:
) en m², del tipo de material y de la temperatura. Si consideramos la temperatura constante (20 ºC), la resistencia viene dada por la siguiente expresión:
 ) en m, de su sección (
) en m, de su sección ( ) en m², del tipo de material y de la temperatura. Si consideramos la temperatura constante (20 ºC), la resistencia viene dada por la siguiente expresión:
) en m², del tipo de material y de la temperatura. Si consideramos la temperatura constante (20 ºC), la resistencia viene dada por la siguiente expresión: 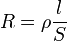
Influencia de la temperatura
La variación de la temperatura produce una variación en la resistencia. En la mayoría de los metales aumenta su resistencia al aumentar la temperatura, por el contrario, en otros elementos, como el carbono o el germanio la resistencia disminuye.
Como ya se comentó, en algunos materiales la resistencia llega a desaparecer cuando la temperatura baja lo suficiente. En este caso se habla de superconductores.
Experimentalmente se comprueba que para temperaturas no muy elevadas, la resistencia a un determinado valor de t ( ), viene dada por la expresión:
), viene dada por la expresión:
 ), viene dada por la expresión:
), viene dada por la expresión: 
donde
 = Resistencia de referencia a 20 °C.
= Resistencia de referencia a 20 °C. = Coeficiente Olveriano de temperatura.
= Coeficiente Olveriano de temperatura. = Diferencia de temperatura respecto a los 20 °C (t-20).
= Diferencia de temperatura respecto a los 20 °C (t-20).
Potencia que disipa una resistencia
Una resistencia disipa en calor una cantidad de potencia cuadráticamente proporcional a la intensidad que la atraviesa y a la caída de tensión que aparece en sus bornes.
Comúnmente, la potencia disipada por una resistencia, así como la potencia disipada por cualquier otro dispositivo resistivo, se puede hallar mediante:
A veces es más cómodo usar la ley de Joule para el cálculo de la potencia disipada, que es:
 o también
o también 
Observando las dimensiones del cuerpo de la resistencia, las características de conductividad de calor del material que la forma y que la recubre, y el ambiente en el cual está pensado que opere, el fabricante calcula la potencia que es capaz de disipar cada resistencia como componente discreto, sin que el aumento de temperatura provoque su destrucción. Esta temperatura de fallo puede ser muy distinta según los materiales que se estén usando. Esto es, una resistencia de 2 W formada por un material que no soporte mucha temperatura, estará casi fría (y será grande); pero formada por un material metálico, con recubrimiento cerámico, podría alcanzar altas temperaturas (y podrá ser mucho más pequeña).
El fabricante dará como dato el valor en vatios que puede disipar cada resistencia en cuestión. Este valor puede estar escrito en el cuerpo del componente o se tiene que deducir de comparar su tamaño con los tamaños estándar y su respectivas potencias. El tamaño de las resistencias comunes, cuerpo cilíndrico con 2 terminales, que aparecen en los aparatos eléctricos domésticos suelen ser de 1/4 W, existiendo otros valores de potencias de comerciales de ½ W, 1 W, 2 W, etc.
Ejercicios
PROBLEMA 1. Una resistencia de 3 ohms y otra de 7 ohms se conectan en serie a una combinación paralelo formada por resistencias de 4 ohms, 6 ohms y 12 ohms, como se indica en la Fig. 1-8. A este circuito se aplica una fem de 50 volts .
Determinar, a) la corriente total de línea y la resistencia total (equivalente) ; b) la caída de voltaje sobre la resistencia de 3 ohms y 7 ohms, y sobre el grupo paralelo; y c) la corriente en cada rama del grupo paralelo.

Fig. 1-8 . Circuito serie-paralelo (problema 1 )


PROBLEMA 2. Cinco resistencias en serie-paralelo están conectadas a una fuente de 100 volts en la forma indicada en la Fig. 1-9. Determinar la resistencia equivalente del circuito, la corriente de línea (total) , la caída de voltaje sobre cada resistencia y la coiriente a través de cada una.
Solución.Primero debe simplificarse el circuito hasta una combimación ser¡e, en cuatro pasos (Fig.1-9 ):
Paso 1 . La resistencia paralelo de la combinación de 5 ohms y 20 ohms es ,
Paso 2 . La resistencia serie del conjunto de 4 ohms y 16 ohms es ,

Fig. 1-9 . Pasos para resolver el circuito serie-paralelo ( problema 2) .
Paso 3. Para las resistencias de 20 ohms y 80 ohms en paralelo,
Paso 4. La resistencia de 16 ohms en serie con la resistencia de 4 ohms es la resistencia total, Rt = 16 ohms + 4 ohms = 20 ohms
Por lo tanto,
La corriente de línea (total) , It = E/Rt = 100 volts/20 ohms = 5 amps
La corriente a través de la resistencia de 4 ohms es la corriente de línea (5 amps) ; por lo tanto la caída de voltaje = IR = 5 amps x 4 ohms = 20 V. La caída de voltaje sobre el resto de la combinación serie-paralelo (resistencias de 5; 20; 16 y 80 ohms) , es por lo tanto, 100 volts - 20 volts = 80 volts. Alternativamente, la resistencia de esta combinación es 16 ohms (paso 3) y por lo tanto la caída de voltaje sobre ella es = IR - 5 amps x 16 ohms = 80 volts. La caída de voltaje sobre la resistencia de 80 ohms es la misma que sobre la combinación total, o sea 80 volts. Por lo tanto, la corriente a través de la resistencia de 80 ohms = 80 volts/80ohms = 1 amp.
La corriente a través de la resistencia de 16 ohms es la diferencia entre la corriente total y la que circula por la rama de 80 ohms, o sea 5 amps - 1 amp = 4 amps.
[Alternativamente, la corriente a través de la resistencia de 16 ohms es la caída de voltaje sobre la combinación serie-paralelo dividido por la resistencia de la rama en la cual está colocada la resistencia de 16 ohms. La caída de voltaje es 80 volts; la resistencia de la rama es 20 ohms (paso 2) . Por lo tanto, la corriente por la resistencia de 16 ohms = 80 volts/20 ohms = 4 amps.]
La caída de voltaje sobre la combinación paralelo de resistencias de 5 y 20 ohms, es la corriente de la rama (4 amps) por la resistencia paralelo (4 ohms, paso 1 ), o sea, 4 amps x 4 ohms = 16 volts. La caída de voltaje sobre la resistencia de 16 ohms = 4 amps (Alternativam., caída de 80 volts - caída de 16 volts = 64 volts.)
Corriente a través de la resistencia de 5 ohms = E/R = 16 volts/5 ohms = 3,2 amps
Corriente a través de la resistencia de 20 ohms = E/R = 16 volts/20 ohms = 0,8 amp
Estas dos corrientes deben sumarse a la corriente de la rama a través de la resistencia de 16 ohms:
3,2 amps + 0,8 amp = 4 amperes (que sirve de prueba) . Esto completa la solucion del circuito.
Referencias Bibliográficas:
Referencias Bibliográficas:
http://es.wikipedia.org/wiki/corriente_electrica
http://es.wikipedia.org/wiki/resistencia_electrica
http://es.wikipedia.org/wiki/resistencia_electrica



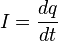
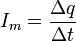
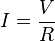
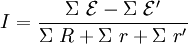
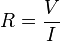





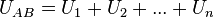



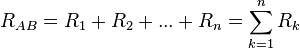
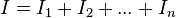


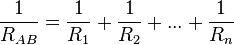





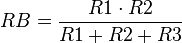




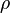 es la
es la 